Векторное и смешанное произведение векторов. - 22 Января 2012 - Шпора по Аналитической геометрии (1семестр / 1 курс)

Главная » » Векторное и смешанное произведение векторов.

17:44

Векторное и смешанное произведение векторов.

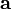Сме́шанное произведе́ние $(\mathbf{a}, \mathbf{b}, \mathbf{c})$ векторов $\mathbf{a}, \mathbf{b}, \mathbf{c}$ — скалярное произведение вектора $\mathbf{a}$ на векторное произведение векторов $\mathbf{b}$ и $\mathbf{c}$ :

$(\mathbf{a}, \mathbf{b}, \mathbf c) = \mathbf{a}\cdot\left(\mathbf{b}\times\mathbf c\right)$ .

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами $\mathbf a, \mathbf b, \mathbf c$ .

Векторным произведением вектора $\mathbf a$ на вектор $\mathbf b$ в пространстве $\R^3$ называется вектор $\mathbf c$ , удовлетворяющий следующим требованиям:

длина вектора $\mathbf c$ равна произведению длин векторов $\mathbf a$ и $\mathbf b$ на синус угла $\varphi$ ; между ними

вектор $\mathbf c$ ортогонален каждому из векторов $\mathbf a$ и $\mathbf b$
вектор $\mathbf c$ направлен так, что тройка векторов $\mathbf{abc}$ является правой.
в случае пространства $\R^7$ требуется ассоциативность тройки векторов $\mathbf{a,b,c}$ .

Обозначение:

$\mathbf c = \left[ \mathbf a \mathbf b \right] = \left[ \mathbf a,\; \mathbf b \right] = \mathbf a \times \mathbf b$

В литературе^[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.

Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.

Просмотров: 664 | Добавил: admin | Рейтинг: 0.0/0

Всего комментариев: 0

Шпора по Аналитической Геометрии (1семестр)

Меню сайта

Наш опрос

Поиск

Статистика