5. Оператор поворота относительно координатной оси Если в предыдущих случаях для вычисления матриц операторов мы могли использовать произвольную систему координат, то для вычисления матрицы оператора поворота без декартовой системы координат обойтись очень трудно. Пусть 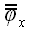 является оператором поворота относительно оси x декартовой системы координат xyz, причем поворот осуществляется по направлению от оси y к z оси. Найдем координаты векторов базиса, подвергнутых действию этого оператора, на рис. 51 они обозначены является оператором поворота относительно оси x декартовой системы координат xyz, причем поворот осуществляется по направлению от оси y к z оси. Найдем координаты векторов базиса, подвергнутых действию этого оператора, на рис. 51 они обозначены 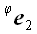 и и 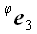 . . 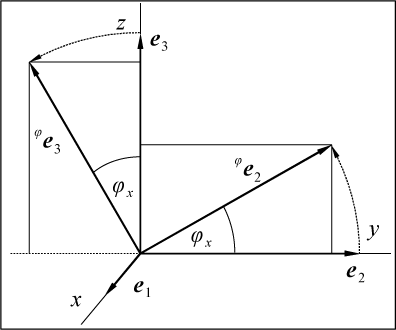 Рис. 51 Рис. 51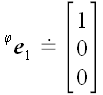 , , 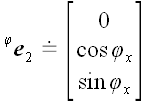 , , 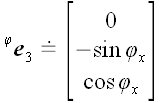 . .
И, следовательно, 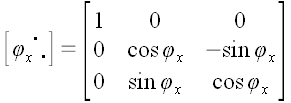 Аналогично можно доказать, что 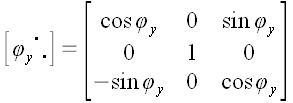 , ,
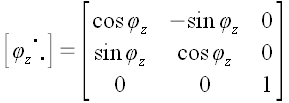 . .
6. Оператор поворота относительно произвольной оси Если нам необходимо выполнить преобразование поворота относительно произвольной оси, не совпадающей ни с одной из координатных осей, мы можем воспользоваться услугами вспомогательной координатной системы 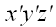 . Если ось . Если ось 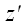 вспомогательной системы координат направить вдоль оси поворота, то матрица оператора поворота в этой системе запишется уже известным образом: вспомогательной системы координат направить вдоль оси поворота, то матрица оператора поворота в этой системе запишется уже известным образом: 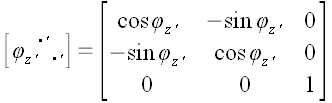 . .
Теперь достаточно воспользоваться известным законом преобразования координат оператора, чтобы найти матрицу его координат в старой системе: 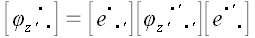 . Общее выражение для матрицы поворота не отличается ни простотой, ни красотой и мы ее здесь не приводим, но и не проводя никаких вычислений, можно сделать некоторые выводы относительно ее свойств. Умножим матрицу . Общее выражение для матрицы поворота не отличается ни простотой, ни красотой и мы ее здесь не приводим, но и не проводя никаких вычислений, можно сделать некоторые выводы относительно ее свойств. Умножим матрицу 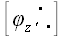 на на 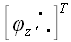 . . 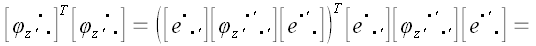
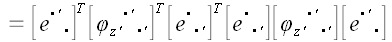 . .
Матрица преобразования  составлена из координат векторов базиса системы составлена из координат векторов базиса системы 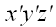 в старой системе координат и, поэтому, в старой системе координат и, поэтому, 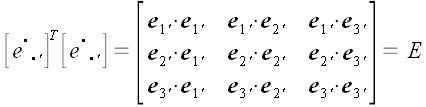 так как система координат является ортонормированной. так как система координат является ортонормированной.
По аналогичным причинам 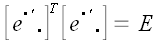 . То, что . То, что 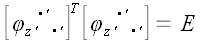 , можно проверить непосредственно. Следовательно, , можно проверить непосредственно. Следовательно,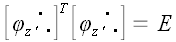 , а это означает, что матрица транспонированная к , а это означает, что матрица транспонированная к 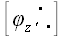 , является к ней обратной: , является к ней обратной: 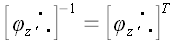 . Матрицы, обладающие таким свойством и соответствующие им операторы, называются ортогональными. Следовательно, матрица оператора поворота, является ортогональной матрицей. Этот факт имеет простое геометрическое объяснение: как бы мы ни поворачивали первоначально ортонормированные векторы базиса, они всегда останутся ортонормированными и, поэтому естественно, что . Матрицы, обладающие таким свойством и соответствующие им операторы, называются ортогональными. Следовательно, матрица оператора поворота, является ортогональной матрицей. Этот факт имеет простое геометрическое объяснение: как бы мы ни поворачивали первоначально ортонормированные векторы базиса, они всегда останутся ортонормированными и, поэтому естественно, что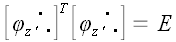 . Однако, все, что мы до сих пор сказали про оператор поворота, справедливо только для ортонормированных систем. . Однако, все, что мы до сих пор сказали про оператор поворота, справедливо только для ортонормированных систем. Пусть теперь 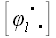 будет оператор поворота в произвольных косоугольных координатах. Перейдем к ортонормированному базису: будет оператор поворота в произвольных косоугольных координатах. Перейдем к ортонормированному базису: 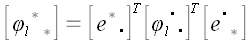 . .
В ортонормированном базисе 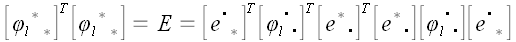 ; ;
Так как 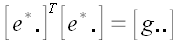 , то , то 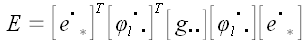 . . Умножим правую и левую части равенства на матрицу 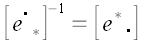 справа и на справа и на 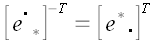 слева. слева. 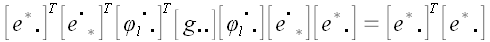 и упрощая далее, получаем и упрощая далее, получаем 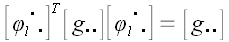 . Умножая справа на . Умножая справа на 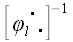 и слева на и слева на 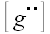 , получим: , получим: 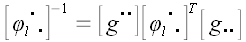 . .
Вообще для произвольного оператора 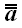 , оператором, сопряженным к нему , оператором, сопряженным к нему 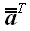 , называется оператор, матрица которого равна , называется оператор, матрица которого равна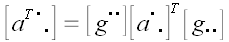 . Сопряженный оператор называется еще транспонированным, поскольку в ортонормированной системе . Сопряженный оператор называется еще транспонированным, поскольку в ортонормированной системе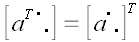 . . Следовательно, обратная матрица произвольного ортогонального оператора и оператора поворота в частности равна матрице сопряженного оператора.
|

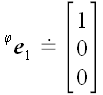 ,
, 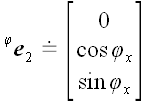 ,
, 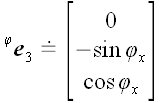 .
.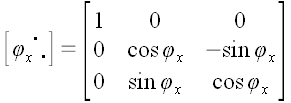
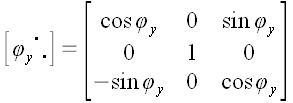 ,
,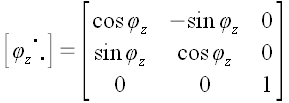 .
.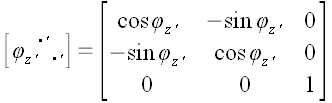 .
.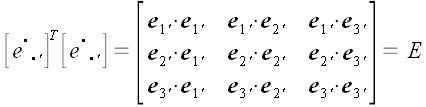 так как система координат является ортонормированной.
так как система координат является ортонормированной.