Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
ОпределениеПусть  есть векторное пространство над полем есть векторное пространство над полем  и и  — базис в — базис в  . . Функция  называется квадратичной формой, если её можно представить в виде называется квадратичной формой, если её можно представить в виде 
где  , а , а  — некоторые элементы поля — некоторые элементы поля  . .
Свойства- Критерий Сильвестра
- Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
- Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
- Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.
- Для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:

- Разность между числом положительных (
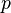 ) и отрицательных ( ) и отрицательных ( ) членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра). ) членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра).
- Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.
- Скалярное произведение векторов
 — симметричная билинейная функция. Соответствующая квадратичная форма — симметричная билинейная функция. Соответствующая квадратичная форма  является положительно определённой, она сопоставляет вектору является положительно определённой, она сопоставляет вектору  квадрат его длины. квадрат его длины. - Квадратичная форма
 на плоскости (вектор на плоскости (вектор  имеет две координаты: имеет две координаты:  и и  ) является знакопеременной, она приводится к каноническому виду ) является знакопеременной, она приводится к каноническому виду  с помощью линейной замены с помощью линейной замены  . .
Примеры квадратичной формы матриц:
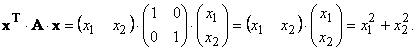
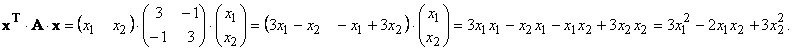
|